D&D 5E Encounter lethality

[clearstream]

Adventuring day XP (DMG 84) suggests the XP characters might get per adventuring day (after adjustment). Using encounter thresholds (DMG 82), one can estimate out how many encounters of a given threshold might be needed for a character to go from level 1 to 20, given a few assumptions (see further below). Dividing XP costs per level (PHB 15) can then suggest a number of adventuring days to reach each level. Here is that table (updated) -



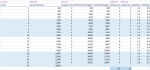
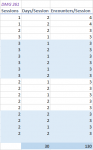
The DMG guidelines for advancement (DMG 261) allow this to be looked at in terms of sessions (updated) -



Chance of death in an encounter type can be assessed against the number of encounters that characters are likely to face, showing how many characters a party of four might need to generate in order to get one to 20th level (updated) -



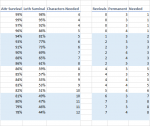
Note the possibly significant role for revival magic. Over a character's entire career, a great many encounters will be faced: magnifying mortality. Here are some background assumptions I made -



For the sake of argument, I called medium and hard encounters "attritional" because they are unlikely to do more than use up resources, and deadly ones "lethal" because they could well result in party deaths. I used the threshold for hard encounters as the XP value for attritional, and the threshold for deadly as the XP value for lethal. In play of course most encounters will fall above thresholds rather than exactly on them. My overall purpose was to answer how lethal an attritional encounter must be, versus a lethal one? To estimate that, a group needs to fix their own assumptions. I'll post this now, and in the following post, below, will discuss some values for lethality and their implications...

 

[clearstream]

Per my first post, assuming a mix of about 2 attritional (medium or hard) encounters to 1 lethal (deadly) per day, taking into account the XP needed to level from 1 to 20, there will need to be about 97 attritional and 33 lethal over a character's career.

What kind of lethality could those encounters reasonably have? Say A is chance of death in attritional encounters, and L is chance in lethal encounters, and using the concept that L should be about an order of magnitude greater than A.

A = 0.1% and L = 1% = ~1/2 characters survives to level 20
A = 1% and L = 10% = ~1/82 characters survives to level 20

Raising anything to the power of 97 or 33 is pernicious. Say L is only double A.

A = 0.1% and L = 0.2% = ~1/1 characters survives to 20
A = 1% and L = 2% = ~1/5 characters survives to 20

The problem here I think, is that L is not palpably more dangerous than A.

Say additionally that characters from tier 2 onward enjoy a chance of being revived (Raise Dead etc) equal to 0.33/0.5/0.66 by tier?

A = 1% and L = 10% = ~1/54 characters survives to 20

As a DM, it feels narratively appropriate to say that deadly encounters are an order of magnitude more lethal than medium or hard ones. It could even be two orders of magnitude -

A = 0.1% and L = 10% = ~1/34 characters survives to level 20, or ~1/23 given revivals from tier 2 on.

Brief Conclusion
The XP construction in D&D means that number of encounters to reach a given level can be estimated. The fact of raising to a power (surviving across those encounters) entails that any palpable difference in the risk of death very likely forces lethal encounters to be less common than attritional ones.

The intents of each group will vary. Some may only be concerned with survival to tier 3. Some may prefer an easier game (five attritional encounters per day is enough to meet the XP requirements) while others prefer more challenging (three lethal encounters per day is enough). Party size affects how often death appears in the ongoing narrative.

Where I think this kind of analysis might help DMs is in suggesting -

• revival is a valuable tool in balancing lethality
• deadly encounters can be palpably more risky than attritional, so long as there are fewer of them
• characters could well face a hundred or more attritional encounters, and a few tens of deadly ones, over their career
• chances of death must be quite low values, probably only a few percent (per character) even in deadly encounters

Many groups perhaps only need to consider the first three tiers of play. Survival rates to level 15 are of course better than those all the way to 20: tables in the OP are banded by tier, with each row showing the expectation to reach that level.

 

[Shiroiken]

I'm not a fan of the encounter guidlines myself, but this was an interesting read.

Something to take into consideration, however, is that most encounters are not going to be at the threshold of the difficulty. For example, a level 5 medium encounter (using your chart) is any value from 500-749 and a hard encounter would be from 750-1099. I would likely use most of those medium encounters at about the 600-700 range and the hard encounters at about 900-1000.

 

[Harzel]

Adventuring day XP (DMG 84) suggests the XP characters might get per adventuring day.

Actually, I think this is not quite right. These are actually the amounts of adjusted XP per character that a party is expected to be able to handle in a "day" (period between long rests). I admit that the DMG text is a little confusing on this point, but here is the whole section that precedes the table.

The Adventuring Day

Assuming typical adventuring conditions and average luck, most adventuring parties can handle about six to eight medium or hard encounters in a day. If the adventure has more easy encounters, the adventurers can get through more. If it has more deadly encounters, they can handle fewer.

In the same way you figure out the difficulty of an encounter, you can use the XP values of monsters and other opponents in an adventure as a guideline for how far the party is likely to progress.

For each character in the party, use the Adventuring Day XP table to estimate how much XP that character is expected to earn in a day. Add together the values of all party members to get a total for the party’s adventuring day. This provides a rough estimate of the adjusted XP value for encounters the party can handle before the characters will need to take a long rest.

The only place in the text that talks about the character "earning" XP is the first sentence of the third paragraph. The rest of this, I believe, makes clear that the table is intended to be a guideline for the maximum amount of combat opposition that a party can handle in a day, as measured by adjusted XP, which in general is greater than awarded XP (if you follow the DMG guidelines).

Further on in your posts you make at least two other assumptions about things that vary quite widely between tables. The first is sessions-to-advance-a-level (for various levels). For many tables, the amount of play time needed to advance is an outcome of play, not a prescribed goal. As such it depends, among other things, on the balance between combat and the other pillars and how or whether XP is awarded for the other pillars, which can vary a lot.

The second is the accuracy of the difficulty implied by the DMG's labels for various encounter XP thresholds. At least on these boards, I believe the general consensus is that those labels might be appropriate for very casual or very inexperienced players, but that many tables will find them a very significant overestimate. My players for instance are definitely not optimizers, power-gamers, nor tactical experts; after several years of play, a couple of them have to be reminded what advantage/disadvantage is. Nevertheless, they typically trounce anything up to the 'deadly' threshold. They may get a little nervous, but they're really in no danger of anyone actually dying.

So, with due respect for the work you put into your calculations, I think your results are probably of limited applicability.

 

[clearstream]

Actually, I think this is not quite right. These are actually the amounts of adjusted XP per character that a party is expected to be able to handle in a "day" (period between long rests). I admit that the DMG text is a little confusing on this point, but here is the whole section that precedes the table.The only place in the text that talks about the character "earning" XP is the first sentence of the third paragraph. The rest of this, I believe, makes clear that the table is intended to be a guideline for the maximum amount of combat opposition that a party can handle in a day, as measured by adjusted XP, which in general is greater than awarded XP (if you follow the DMG guidelines).Further on in your posts you make at least two other assumptions about things that vary quite widely between tables. The first is sessions-to-advance-a-level (for various levels). For many tables, the amount of play time needed to advance is an outcome of play, not a prescribed goal. As such it depends, among other things, on the balance between combat and the other pillars and how or whether XP is awarded for the other pillars, which can vary a lot.The second is the accuracy of the difficulty implied by the DMG's labels for various encounter XP thresholds. At least on these boards, I believe the general consensus is that those labels might be appropriate for very casual or very inexperienced players, but that many tables will find them a very significant overestimate. My players for instance are definitely not optimizers, power-gamers, nor tactical experts; after several years of play, a couple of them have to be reminded what advantage/disadvantage is. Nevertheless, they typically trounce anything up to the 'deadly' threshold. They may get a little nervous, but they're really in no danger of anyone actually dying.So, with due respect for the work you put into your calculations, I think your results are probably of limited applicability.

I agree with you that there are discrepancies and indeed different ways to understand and use the DMG guidelines. That said, I believe the core of my argument is robust and that in the end those are peripheral issues. The core might be summarised -

• There is some chance of character death in a deadly encounter
• Under the ordinary XP construction of D&D, characters will face more than one encounter of each type in order to level from 1 to 20
• The chance of surviving those encounters can be approximated as (1-c)^f where c is the individual encounter chance of death and f is the number of encounters faced
• From there, the number of characters needed at level 1 for each surviving to level 20 is able to be estimated

I then call attention to the fact that, if there is indeed only a slim or no chance of death in non-deadly encounters, and indeed a palpably greater chance of death in deadly encounters, then it is right to say that c will be pronouncedly larger in the latter. You see what I mean? Without disagreeing with you (I don't) you can see that my central claims aren't impacted by those matters. Whatever values a DM thinks prevail in their campaign, the central claim applies equally well to those.

 

[dave2008]

Interesting work, keep at it.

 

[Blue]

Encounter lethality is only partially dependent on that encounter. A part (possibly even the largest part) is the condition of the PCs as they enter it in terms of resources available.

I can run 12 medium encounters in a day and kill off PCs because they ran out of spells, feature uses, HD, etc. I can also run two deadly+ encounters in a day and they PCs come out just fine because they went in with full resources and weren't afraid to spend them.

While attrition battles to the death are far from the only way of structuring win-vs-lose for D&D combats, it is the most common of them and what you're addressing here. Any attempt to label a particular combat with a lethality, expecting it to be the same regardless of if it's the only battle the PCs are in that day or if they are going in low on resources already is doomed to be inaccurate.

 

[clearstream]

Encounter lethality is only partially dependent on that encounter. A part (possibly even the largest part) is the condition of the PCs as they enter it in terms of resources available.

I can run 12 medium encounters in a day and kill off PCs because they ran out of spells, feature uses, HD, etc. I can also run two deadly+ encounters in a day and they PCs come out just fine because they went in with full resources and weren't afraid to spend them.

While attrition battles to the death are far from the only way of structuring win-vs-lose for D&D combats, it is the most common of them and what you're addressing here. Any attempt to label a particular combat with a lethality, expecting it to be the same regardless of if it's the only battle the PCs are in that day or if they are going in low on resources already is doomed to be inaccurate.

The approach taken seems to do a reasonable job of capturing what will happen across many encounters. It asks what sort of range are we talking about, for number of encounters in a character's career? And shows that if on average (some will be more dangerous, some less, as you point out) the chance of death is c, the number of encounters magnifies that exponentially. It reinforces some of the levers, for a DM. (Ratio of encounter types, encounter lethality, availability of revival magic, non-encounter XP.)

Where I think it can become especially interesting is reversing out values from observations. I'll post up the sheet once I've tidied it up. One surprising thing is how low the chance of death must be, on a per character per encounter basis, to give characters reasonable hope of reaching level 20; which chimes with what DMs described in an earlier thread I created, asking about frequency of death in posters' campaigns.

 

[Blue]

The approach taken seems to do a reasonable job of capturing what will happen across many encounters.

No, it really doesn't. I laid out specifics which you ignored. You're just handwaving them away by claiming what you have is "reasonable"; not addressing the point I made in the least.

Okay, let's take the most absurd case: Take a tough encounter. Case A: That encounter is your only fight of the day for 12 days. Case B: You have that fight 12 times on the same day with a short rest after the 4th and after the 8th.

VERY different lethality rates. (Unless it's an utter cakewalk.) Yet it's the same number of encounters.

A less extreme set of DMs might find one doing 3-4 encounters per long rest with about 2 short rests, while another does 6-8 encounters per long rest with about 2 short rests. Both reasonable ways to do it, and with the same encounters the second DM will have more casualties as attrition wears down resources.

Again, in this case it's the same number of encounters. But the chance for character death increases the longer it goes on without replenishing resources.

 

[clearstream]

No, it really doesn't. I laid out specifics which you ignored. You're just handwaving them away by claiming what you have is "reasonable"; not addressing the point I made in the least.

Okay, let's take the most absurd case: Take a tough encounter. Case A: That encounter is your only fight of the day for 12 days. Case B: You have that fight 12 times on the same day with a short rest after the 4th and after the 8th.

VERY different lethality rates. (Unless it's an utter cakewalk.) Yet it's the same number of encounters.

A less extreme set of DMs might find one doing 3-4 encounters per long rest with about 2 short rests, while another does 6-8 encounters per long rest with about 2 short rests. Both reasonable ways to do it, and with the same encounters the second DM will have more casualties as attrition wears down resources.

Again, in this case it's the same number of encounters. But the chance for character death increases the longer it goes on without replenishing resources.

Ah, right. I agree that the chance will fluctuate. For example, I believe from experience that the average rate per encounter declines with tier and have considered incorporating that as a factor.

Say we have 12 different values for c - 0.1, 0.1, 0.025, 0.05, 0.01, 0.003, etc - modelling your differing rates. The question is whether that mathematically differs from using an average of those rates? In some instances it is obvious that it does not, e.g. the sum of 1 then 2 then 3, each times 97, is the same as 2 then 2 then 2, each times 97. The estimate is based on using (1-c)^f to get a survival chance over f encounters. Perhaps you're saying that there will exist a mathematical difference between using that simple formula with a constant for c, versus using a summation. Is that right?

I can prove that one way or another, by inserting random numbers for c on a per encounter basis, creating a summation and comparing. I'll do that and come back to you.

Perhaps you are instead or also saying that our second DM always uses fewer rests per encounter, so all their encounters are more lethal, and that is your main concern? That amounts to saying second DM is using a higher value for c, and does not challenge the argument. It only says pick a larger value for c, for that DM.


[EDIT: Intuitively, a summation shouldn't differ from exponentiation using the average. In the end, they're both a series of multiplications. But I was thinking of creating a Monte Carlo sim for it, and generating an array of c's can tie into that.)